bcgen with seasonally resolved SST/SIC

[dstiller]

Hi,

I am trying to run AMIP-style experiments with the FHIST compset. However, the SST/SIC timeseries I want to prescribe consists of seasonal means (4 timesteps per year) while bcgen requires monthly means. Is there a standard way to prescribe seasonally resolved SST/SIC?

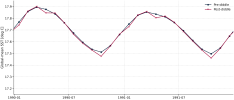
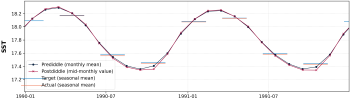
One straightforward approach would be to linearly interpolate to monthly resolution, then apply bcgen. This might work well for MAM and SON. However, for DJF and JJA, we would presumably miss some of the temperature extremes in summer and winter (i.e., the reason to use bcgen in the first place).

Thanks,
Dominik

 

[dstiller]

I've tested linear and cubic spline interpolation of the seasonal means to monthly resolution. The following plots show global-mean SSTs for a two-year period, pre-diddle (input to bcgen) and post-diddle (output of bcgen).
Linear interpolation:


Cubic spline interpolation:


The pre-diddle SSTs with cubic spline interpolation have a more realistic annual cycle than those with linear interpolation. Also, the monthly means occasionally exceed the seasonal means (which is good), this doesn't happen with linear interpolation.

However, the April post-diddle values have an unphysical dip, which is not present in the pre-diddle values.

 

[dstiller]

Please ignore the previous post, I applied the wrong land-sea mask during plotting. Here's the correct version, including SIC.

Linear interpolation:


Cubic spline interpolation:


The kinks created by linear interpolation means that the post-diddle value needs to overshoot the target by a lot. The results with spline interpolation are much smoother and more physical-looking, at least in the global mean. Also, at least for SST, the monthly means exceed the seasonal means, as one would expect.

I would still like to hear if there is a standard way to prescribe seasonally resolved SST/SIC, but spline interpolation seems like a reasonable way.

 

[hannay]

I am not aware of a standard method to prescribe seasonal resolved SSTs, but your approach seems reasonable to me.
A test would be to run a year and to see if the SSTs you obtain reproduce the seasonal observed SSTs,

 

[dstiller]

Thanks for the test run suggestion, I will try that.

One problem with spline interpolation is that it does not preserve the means. Therefore, I'm using the Python package "mpsplines" (mean-preserving splines) now, which relaxes the constraint that the interpolated curve has to go through the input points.

Mean-preserving second-order spline interpolation:

 

[dstiller]

I can confirm that the mean-preserving spline method works. The blue lines are the seasonal averages I want to match, the orange lines are the seasonal means from the CAM output of a test run: