There are 32 vertical layers in CAM6 model and the model's top height is ~40 km
One clarification - are these the layer top heights, or layer centers?
One clarification - are these the layer top heights, or layer centers?
Thanks!!Hi Dharmendra,
Let me know if this doesn't answer your question, but I think what you're asking about boils down to the difference between pver and pverp in the code. If there are 32 layers, that means that there are 32 midpoints and 33 top points. Any time a quantity is indexed with pver, it's at the midpoint; if it's indexed with pverp (which is pver + 1), it's at the top of the layer.
Hope that helps.
Courtney
Thank you so much for a very nice explanation. I am wondering if you could tell me why we should consider scaling 7km for hight.Quoting the height of the top is an approximation since the model grid is in hybrid-sigma coordinates, which are coordinates of constrant pressure by the time you're at the model top. In the CAM output you can see the variables hyam and hybm which are the hybrid coefficients for the layer centers, and hyai and hybi which are the hybrid coefficients for the layer interfaces.
The coefficients for the top interface level are hyai ~ 0.0023 and hybi = 0, so the pressure level of this top interface is 1000*hyai + PS*hybi ~2.3hPa. You could convert this into an approximate height assuming a scale height of H~7km and using z = -Hln(2.3/1000.) ~ 43km.
The coefficients for the top mid-level are hyam ~ 0.0036, hybm = 0, so the pressure of the top mid-level is 1000*0.0036 = 3.6hPa. Converting this to height assuming a scale height of 7km gives 39.4km.
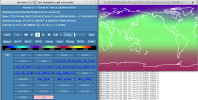
But these are only approximate because the exact height of the top mid-level and interface will depend on the surface pressure and temperatures below following the hypsometric equation. See the screenshot below which shows a snapshot of the geopotential height of the top mid-level of CAM.
View attachment 4050
Thanks!From hydrostatic balance, we have, dp/dz = -rho*g. From the ideal law, we have rho = p/RT, so
(1/p)dp/dz = -g/RT
dln(p)/dz = -g/RT
Integrate this with respect to z from surface to height z and you get
p(z) = ps*exp(-gz/RT)
So pressure is falling off with an e-folding distance of RT/g (the scale height) and if you plug in typical values you get somewhere of the order 7-8km or so. It's obviously an approximation because T varies.
Hi islas,Thanks!