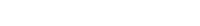Hi everyone!
I run F_2000 in CESM1.2.1 for 30 years and I want to know whether it finishes spinning up. So, I calculate FSNT-FLNT (global) to judge. But I don't think it tends to be stable. The figure is placed below.
So, does anyone know the method I used is right or whether there is a better way to judge?
I run F_2000 in CESM1.2.1 for 30 years and I want to know whether it finishes spinning up. So, I calculate FSNT-FLNT (global) to judge. But I don't think it tends to be stable. The figure is placed below.
So, does anyone know the method I used is right or whether there is a better way to judge?