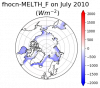
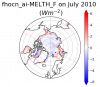
1. Is fhocn the same as Fbot defined in equ. (124) from the science guide?
Fbot=−ρ_w c_w c_h u∗ (Tw−Tf) (124)
2. I am working with the CESM-LE. Fcb (conductive heat flux at the bottom surface) variable is not available as an output. Can we calculate the Fcb with the difference between MELTH_F (Melt Heat Flux from Coupler from the ocean model) and fhocn? or the difference between MELTH_F and fhocn_ai?
Thank you for your help!
Fbot=−ρ_w c_w c_h u∗ (Tw−Tf) (124)
2. I am working with the CESM-LE. Fcb (conductive heat flux at the bottom surface) variable is not available as an output. Can we calculate the Fcb with the difference between MELTH_F (Melt Heat Flux from Coupler from the ocean model) and fhocn? or the difference between MELTH_F and fhocn_ai?
Thank you for your help!